III. RESULTS
Outer-Belt Asteroids and Long-Term
Chaotic Motion
We present our results for the 25 outer-belt
J
(11.86 yr). The
Lyapunov time T
L
is shown in column 3, while
the predicted escape time T
e
, in units of 10
6
T
J
,
is in column 4. T
e
using b=1.74 and a=1.30. These values were
determined from the semimajor axis survey
results of this study, presented below. They
agree with the values found in LFM for aster-
oid orbits interior to Jupiter. The 25 orbits fall
into three categories, as denoted in column 5.
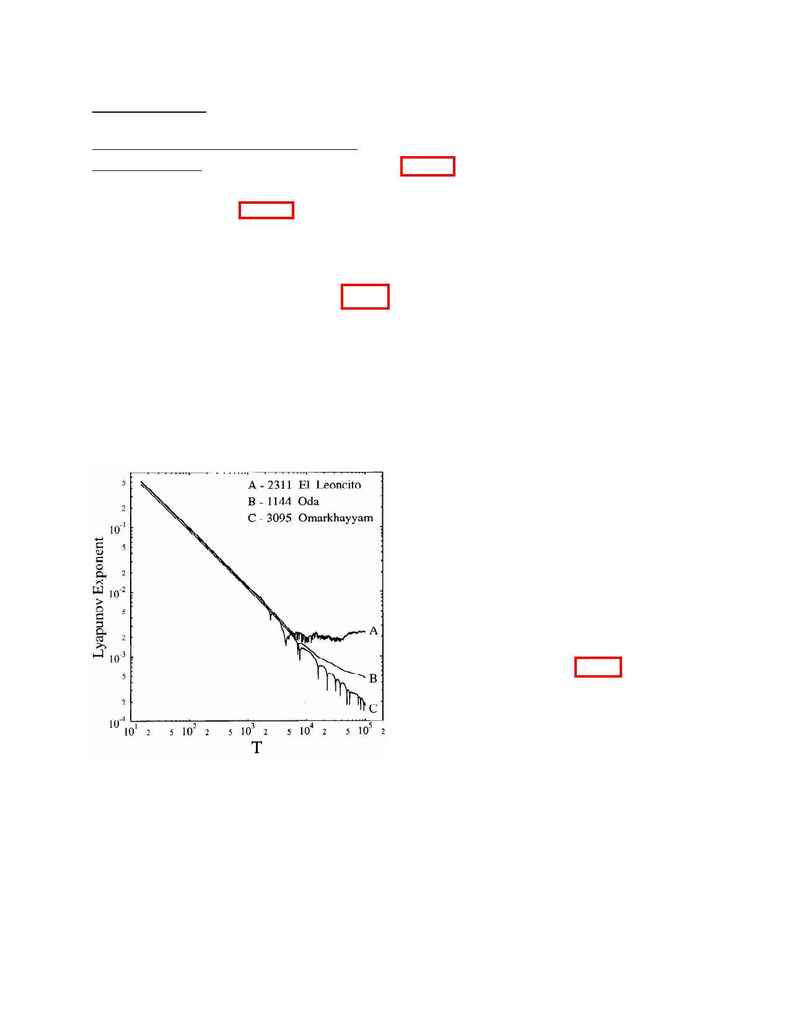
An "A" signifies a clearly chaotic orbit, where
the Lyapunov exponent as a function of time
appears to have leveled off to a nonzero value.
A typical plot of
in such a case is shown in
appears to be
leveling off but the integration was not long
enough to determine a value. The values of T
L
calculated for these orbits are therefore lower
limits. A typical plot for this case is shown in
Figure 1, curve B. A "C" in column 5 means
that the orbit was quasiperiodic (or very weakly
chaotic at best), where the Lyapunov exponent
is asymptotically zero (or nearly zero). Curve
C of Figure 1 shows
vs. t for a typical orbit of
this type. The actual T
L
for these orbits is very
large. We could have performed longer inte-
grations and, possibly, thereby removed some
of the > signs from columns containing T
L
and
T
e
i.e., converted class C into class B, or
class B into class A. This would be a noble
deed, but not an especially valuable use of time
because our real interest and concern centers
on just those minor planets with short Lyapu-
nov times.
An important characterization of the T
L
-T
e
L
and therefore relate it to physical
systems. In data obtained from LFM, we found
that the distribution of residuals in log T
e
for
the Jupiter-Sun system and asteroid orbits
inside Jupiter's orbit was consistent with a
Gaussian shape with standard deviation
=
0.98. Thus, for a given population of objects,
some nonzero percentage would be expected
to lie in the tail of the distribution. Take for
example the asteroid in Table II with the
Chaotic Motion in the Outer Asteroid Belt
page 5
Figure 1.
Typical behavior of the Lyapunov exponent
as a function of time (in Jovian periods), illustrating three
types. The curve labeled A is strongly chaotic; an
approximate value for
is quickly found. Curve B is
"possibly-chaotic," and further integratio n is required to
determine the asymptotic value of
. Curve C represents a
typical quasiperiodic (or at best very weakly chaotic) orbit.
