Galil Motion Control note 3312 Page 4
The S curve digital filter is modeled in the z plane by this equation:
F z
z
z
e
T
( )
/
=
-
-
where T is the sample time, fixed at 2 milliseconds on the DMC-1500, and
is the time
constant. The IT command sets the pole of the S curve filter:
1
-
=
-
IT
e
T /
Solving the above equation for the time constant
, and substituting the 2 millisecond
sample time for T:
=
-
-
.
ln(
)
002
1
IT
The equation above shows how the IT setting affects the S curve filter's time constant
.
The IT setting on the DMC-1500 defaults to 1.0, which results in an infinitely short
time constant and no filtering effect. Decreasing IT causes the time constant to increase,
and the acceleration and deceleration is then smoother. Substitute VT for IT in the
above equation to determine the vector acceleration time constant.
The time constant of the S curve filter changes the amount of time to ramp up and ramp
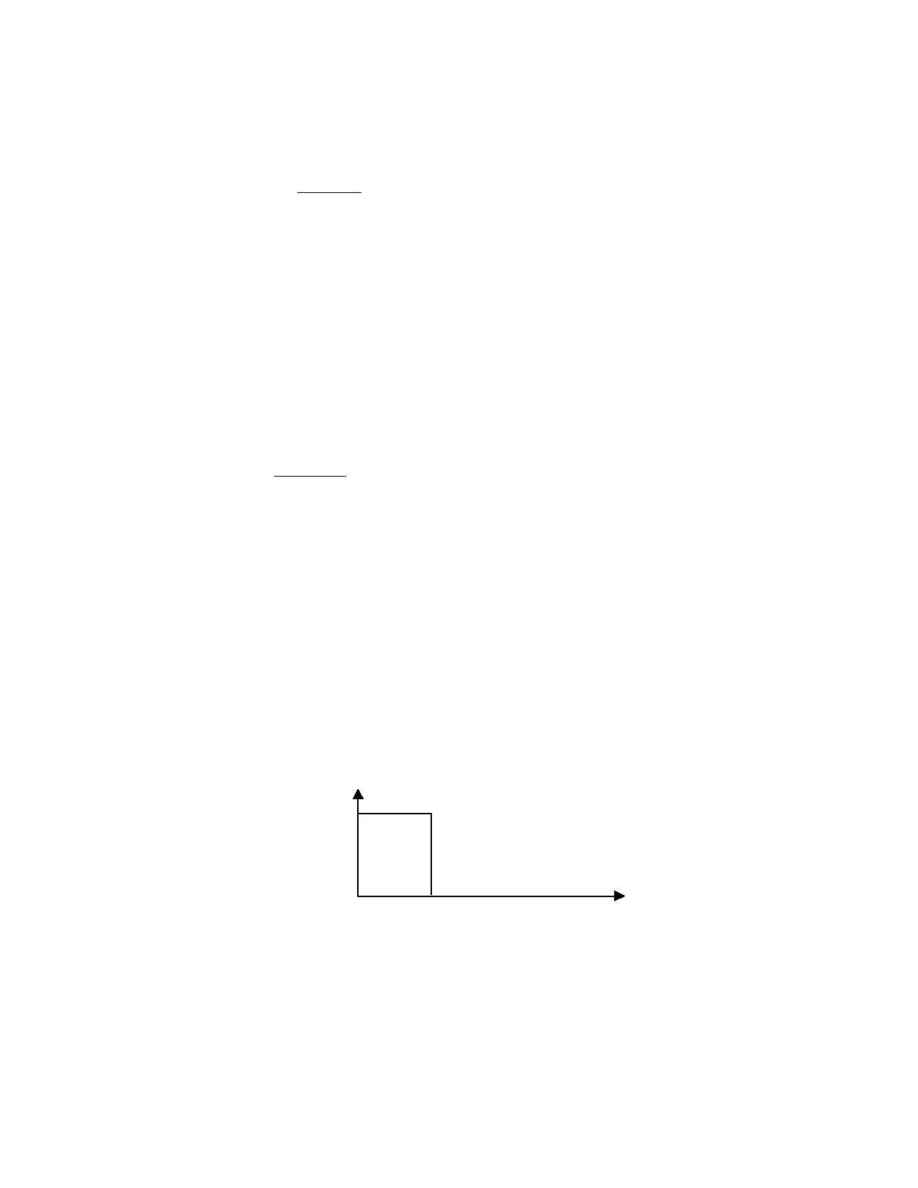
down the acceleration in our motion example. If the S curve time constant were 0, then
the acceleration ramps up and down nearly instantaneously:
Acceleration
400,000 cts/s
2
time
.25 sec
0
If we decrease the IT value the time constant will increase, and the amount of time for
the acceleration to reach the set value will also increase:
