Astronomical Applications Department, U.S. Naval Observatory Precession Maple Page 17
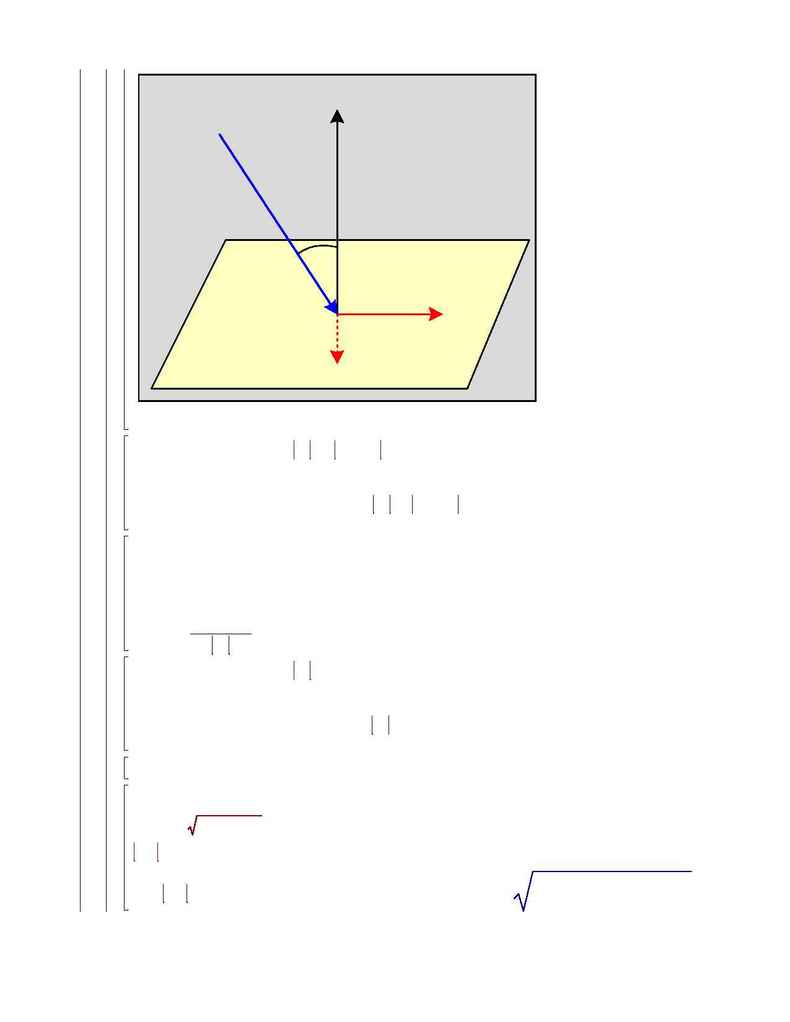
N
P
dF
dF
dS
Figure 3
The force on an area element
dS
is
=
(
)
mat
,
dF
perp
dF
parallel
P dS '
'
( )
cos
(
)
mat
,
(
)
+
1
A
C
( )
cos
(
)
-
1
A
C
( )
sin
=
dF
perp
dF
parallel
P dS
( )
cos
(
)
+
1
A
C
( )
cos
(
)
-
1
A
C
( )
sin
where
F
perp
and
F
parallel
are the component perpendicular and parallel to
dS
,
is the angle
between
P
and the (unit) surface normal
N
, and
A
C
is the albedo of the cone surface. From
Figure 3, we see that
<
(
)
dot
,
P N
0
for our problem. Hence,
=
cos
-
cos
(that is,
=
cos
-
(
)
dot
,
P N
P
) and we have
=
(
)
mat
,
dF
perp
dF
parallel
P dS
( )
cos
(
)
mat
,
-
(
)
+
1
A
C
( )
cos
(
)
-
1
A
C
( )
sin
=
dF
perp
dF
parallel
P dS
( )
cos
-
(
)
+
1
A
C
( )
cos
(
)
-
1
A
C
( )
sin
The magnitude of
dF
is
:=
dFpp
(
)
convert
,
(
)
evalm
(
)
rhs %
vector
(
)
simplify
,
(
)
dot
,
% %
=
assume
real
=
dF
(
)
rootfunc
,
,
,
% collect cos factor
=
dF
( )
signum P P
(
)
signum dS dS
(
)
signum
( )
cos
( )
cos
+
4
( )
cos
2
A
C
(
)
-
A
C
1
2
Page 17
