From:
M. A. Murison
USNO/FAME-TM98-01
To:
Distribution
March 26, 1998
Subj:
Solar Wind and Radiation Effects on the Spin Dynamics of FAME
1 Introduction
[ RDR memo
1
cylindrically symmetrical model, calculated radiation forces and torques on conical
and flattop surfaces, getting precession rates. Introduced idea of nulling precession by adjusting
"skirt" angle. Argues for faster spin.] [ John's two memos. ]
[1. Full dynamical model. 2. Solar wind. 3...]
2 Equations of Motion for a Rigid Body
The equations of motion of a rigid body can be written
2
(1)
I
x
d
dt
W
x
+
I
z
-
I
y
W
y
W
z
-
K
x
=
0
I
y
d
dt
W
y
+
(I
x
-
I
z
)
W
x
W
z
-
K
y
=
0
I
z
d
dt
W
z
+
I
y
-
I
x
W
x
W
y
-
K
z
=
0
where the frame of reference is fixed to the body with origin at the center of mass (the body frame).
The
axes are coincident with the principal axes of the body (i.e., the axes for which the inertia
(x, y, z)
tensor is diagonal).
are the principal
I
x
, I
y
, I
z
moments of inertia of the body,
are the
W
x
,
W
y
,
W
z
angular velocities of the body about the principal axes,
and
are the components of the external
K
x
, K
y
, K
z
torques acting on the body as viewed in the body
frame of reference.
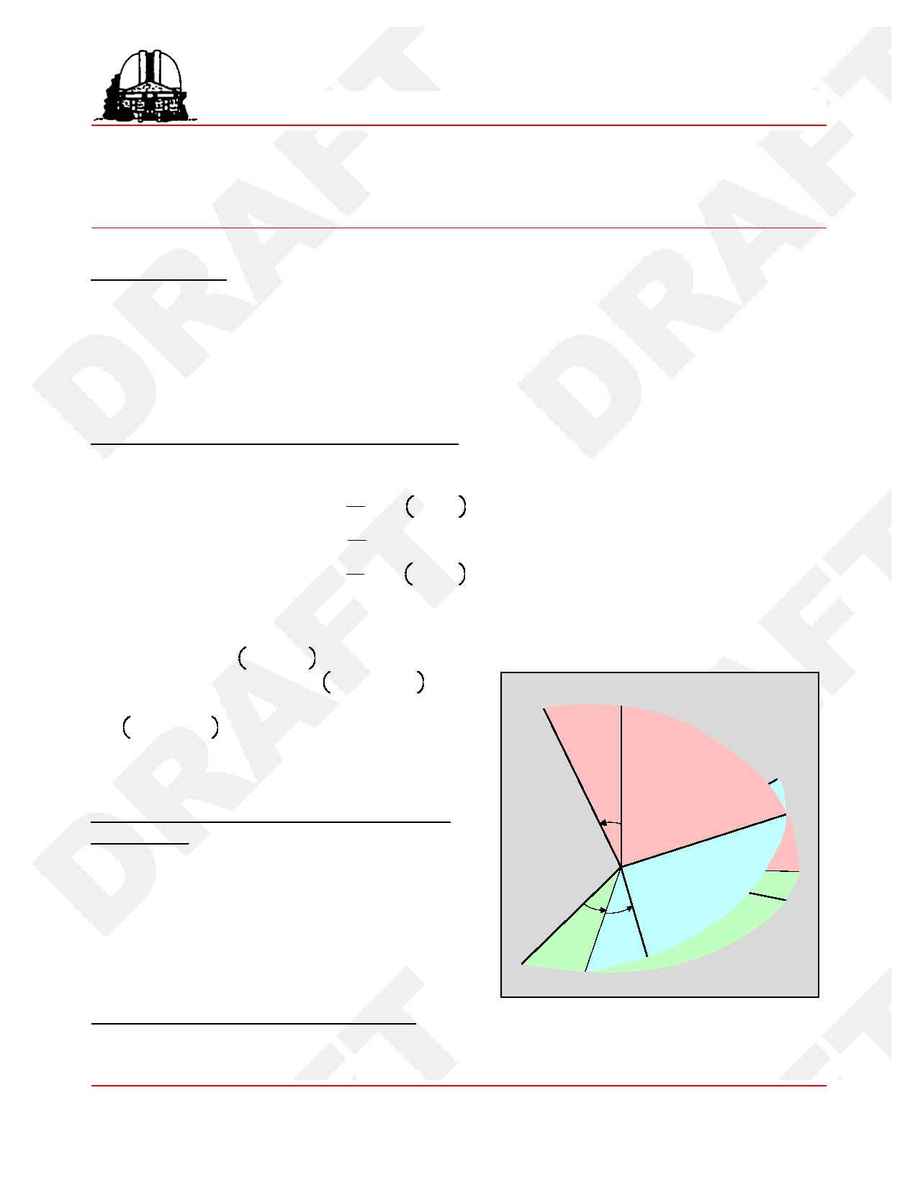
2.1 Euler Angle Rotations between the Fixed and
Body Frames
The particular Euler angles
shown in Figure 1
(
w, y, h)
are a convenient choice. The transformation matrix
(2)
`(w, y, h)
=
`
z
(
h) `
x
(
y) `
z
(
w)
which rotates the fixed coordinate frame
to
(X, Y, Z)
the body frame,
page 1 of 10
U.S. Naval Observatory
Technical Memorandum
D:\dynamics\precession\TechMemo\PrecessionMemo.lwp
X
Y
Z
z
x
y
Figure 1
2
e.g., H. Goldstein (1980). Classical Mechanics, 2nd edition, Addison-Wesley.
1
R.D. Reasenberg (1997). "Effects of Radiation Pressure on the Rotation of FAME", SAO-TM97-03.
