Astronomical Applications Department, U.S. Naval Observatory Precession Memo Page 8
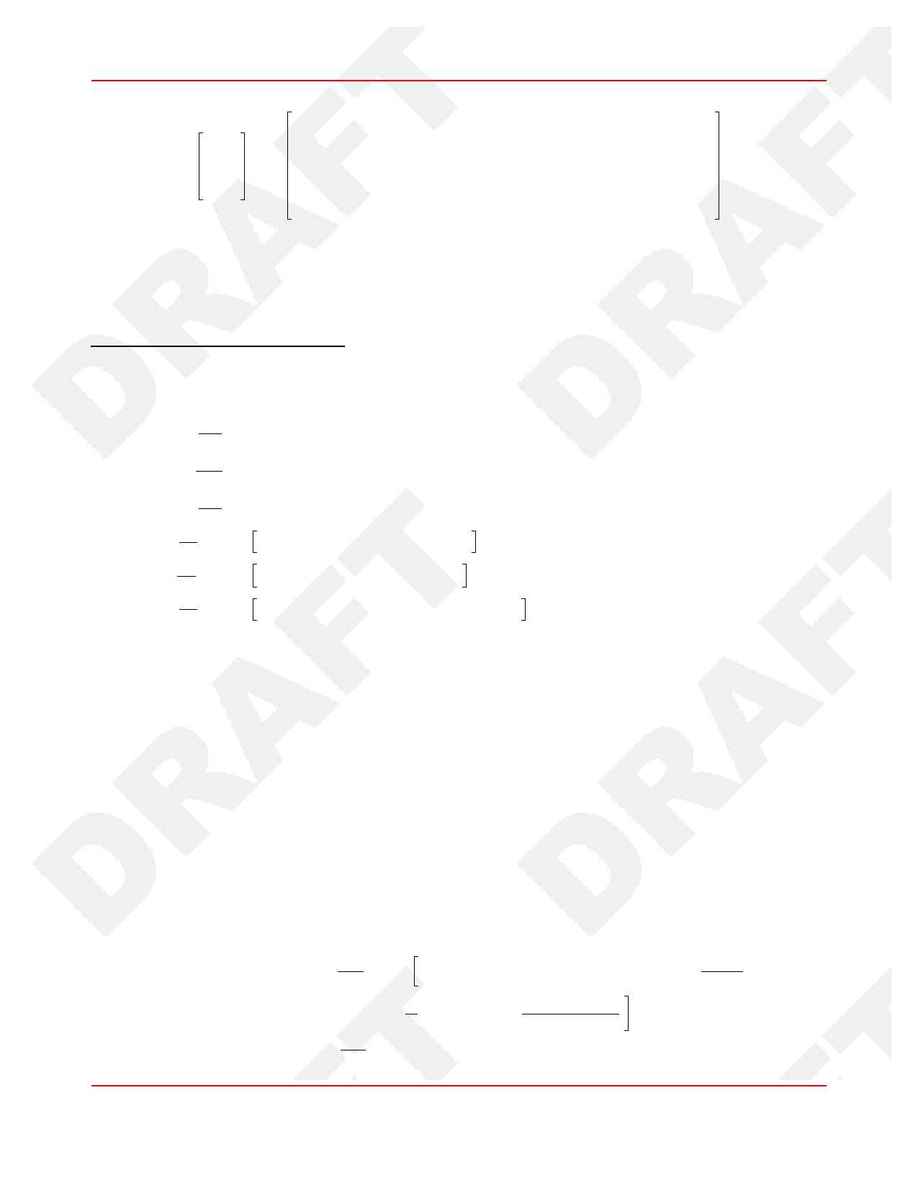
(39)
K
x
K
y
K
z
=
W
o
X
(cos
y cos h sin v
+
sin
h cos v)
+
o
Y
(sin
h sin v
-
cos
y cos h cos v)
-
o
Z
cos
h sin y
o
X
(cos
h cos v
-
cos
y sin h sin v)
+
o
Y
(cos
h sin v
+
cos
y sin h cos v)
+
o
Z
sin
h sin y
0
where
(40)
W h
oPa
2
h (1
-
A
T
)(
-
o
X
sin
y sin w
+
o
Y
sin
y cos w
-
o
Z
cos
y)
and where
is the flattop ("Top") albedo.
A
T
4 The Equations of Motion
Now we may substitute the torque contributions from the cone surface and from the flattop surface,
eqs. (37) and (39), into the equations of motion, eqs. (13). Doing so, we find, after some algebra, that
(41)
d
w
dt
=
W
w
d
y
dt
=
W
y
d
w
dt
=
W
w
sin
y d
dt
W
w
=
(1
-
b) W
h
-
(1
+
b) cos y W
w
W
y
+
K
1
(
a, b, h,
a , A
C
, A
T
,
w, y
)
d
dt
W
y
=
b cos y W
w
2
-
(1
-
b) W
h
W
w
sin
y
+
K
2
(
a, b, h,
a , A
C
, A
T
,
w, y
)
sin
y d
dt
W
h
=
(1
+
b cos
2
y) W
w
-
(1
-
b) cos y W
h
W
y
+
K
3
(
a, b, h,
a , A
C
, A
T
,
w, y
)
where
(42)
K
1
(
a, b, h,
a , A
C
, A
T
,
w, y
)
h G
(
a, b, h,
a , A
C
, A
T
)
$ g
1
(
w, y
)
K
2
(
a, b, h,
a , A
C
, A
T
,
w, y
)
h G
(
a, b, h,
a , A
C
, A
T
)
$ g
2
(
w, y
)
K
3
(
a, b, h,
a , A
C
, A
T
,
w, y
)
h G
(
a, b, h,
a , A
C
, A
T
)
$ g
3
(
w, y
)
(43)
g
0
(
w, y
) = -
o
X
sin
w sin y
+
o
Y
sin
y cos w
-
o
Z
cos
y
g
1
(
w, y
) =
g
0
(
w, y
)
$ (o
X
cos
w
+
o
Y
sin
w)
g
2
(
w, y
) =
g
0
(
w, y
)
$ (o
X
cos
y sin w
-
o
Y
cos
y cos w
-
o
Z
sin
y)
g
3
(
w, y
) = -
g
1
(
w, y
)
cos
y
(44)
G
(
a, b, h,
a , A
C
, A
T
) =
G
C
(
a, b, h,
a , A
C
) +
G
T
(
a, h, A
T
)
G
C
(
a, b, h,
a , A
C
)
=
oP
I
xy
(b
-
a) (1
-
A
C
+
2 A
C
cos
2
a)(h sin a
+
a cos
a) a
+
b
sin
a
-
1
3
(3
+
A
C
) cos
a a
2
+
a b
+
b
2
sin
a
G
T
(
a, h, A
T
)
=
oP
I
xy
(1
-
A
T
) a
2
h
page 8 of 10
