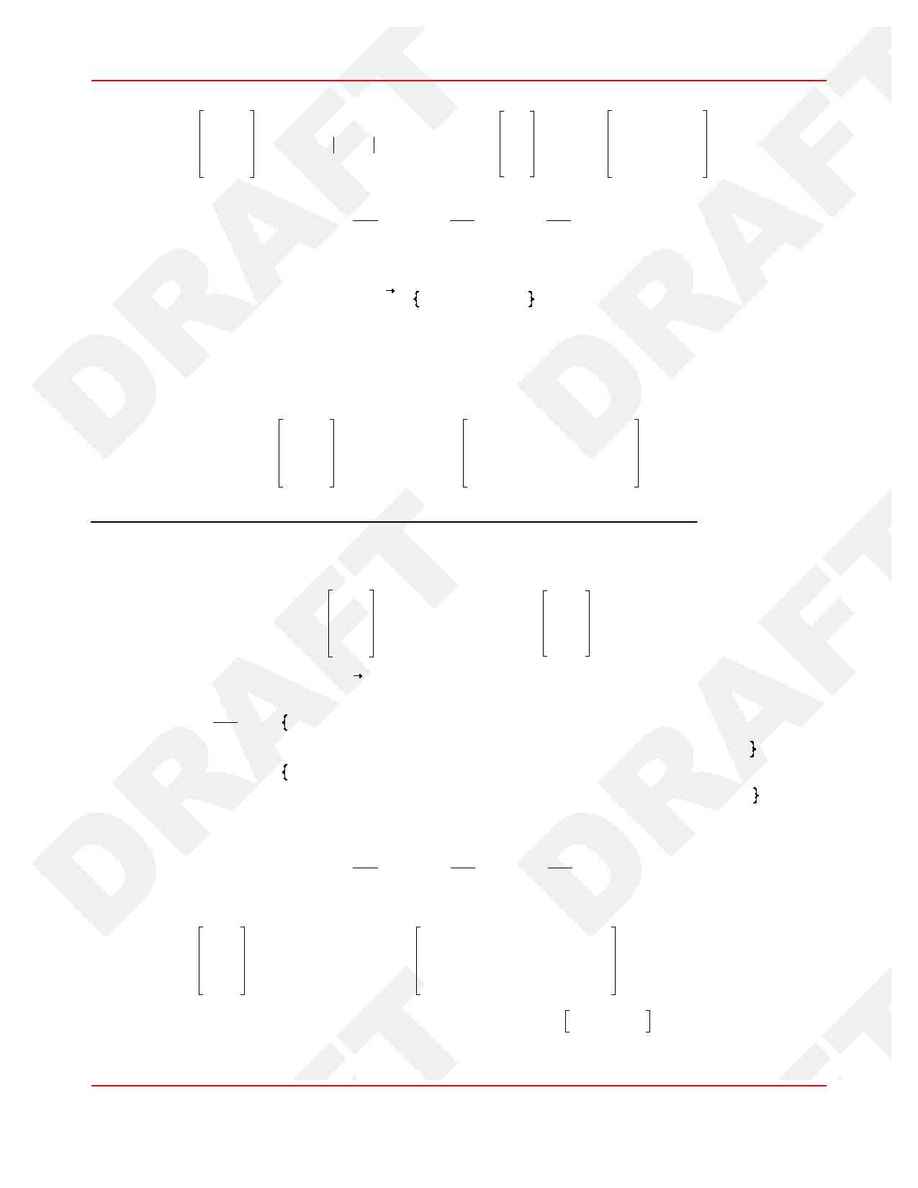
(22)
dF
q
dF
g
dF
a
=
P $ d
S $ cos c $
(1
+
A) cos
c $
0
0
1
+
(1
-
A)
o
q
o
g
o
a
-
cos
c
where
(23)
o
q
h
P
q
P
o
g
h
P
g
P
o
a
h
P
a
P
For simplicity, we now assume that the pressures are always incident on the "top" of the conical sur-
face, that is,
(24)
P c
`
3
x P^ $ N^
<
0
Then we may define the incidence angle
(see Fig. 3),
(25)
cos
x h
-
(P^ $ N^)
= -
cos
c
The infinitesimal force components, eqs. (22), become, after some simplification,
(26)
dF
q
dF
g
dF
a
=
P $ d
S $ cos x $
(1
-
A)
o
q
(1
-
A)
o
g
(1
-
A)
o
a
-
2 A cos
x
3.3 Force and Torque Components Due to Radiation Pressure on the Cone Surface
Let the pressure vector components in the fixed frame be
. Then the components in the
(P
X
, P
Y
, P
Z
)
conical frame are
(27)
o
q
o
g
o
a
=
`(a , g)
-
1
`(w, y, h)
o
X
o
Y
o
Z
Since
, the component of along , we have, from eq. (27),
P^ $ N^
=
P
a
P
a^
(28)
cos
x
= -
P
a
P
= -
cos
a [cos g (cos h cos w
-
sin
h cos y sin w)
-
sin
g (sin h cos w
+
cos
h cos y sin w)]
+
sin
a sin y sin w o
X
-
cos
a [cos g (cos h sin w
+
sin
h cos y cos w)
-
sin
g (sin h sin w
-
cos
h cos y cos w)]
-
sin
a sin y cos w o
Y
-
[cos
a (cos g sin h sin y
+
sin
g cos h sin y)
+
sin
a cos y] o
Z
where we have defined
(29)
o
X
h
P
X
P
o
Y
h
P
Y
P
o
Z
h
P
Z
P
We are now in a position to integrate eqs. (26) over the surface of the cone,
(30)
F
q
F
g
F
a
=
P
░
0
2
o
░
f
f
+
S
cos
x $
(1
-
A
C
)
o
q
(1
-
A
C
)
o
g
(1
-
A
C
)
o
a
-
2 A
C
cos
x
$ q sin a dq dg
where
is the albedo of the conical surface, eq. (27) is used for
, eq. (28) is used for
A
C
o
q
,
o
g
,
o
a
, and the integration limits are defined in Figure 2. The torque, in the conical coordinate frame,
cos
x
is then
page 6 of 10
