It is easy to show that the equation for the conical surface is
(14)
tan
a
=
r
-
a
h
-
z
or
(15)
x
2
+
y
2
-
[a
+
(h
-
z) tan
a]
2
=
0
The body frame coordinates are obtained from the conical coordinates via
(16)
x
=
q sin a cos g
y
=
q sin a sin g
z
=
h
+
a
tan
a
-
q cos a
Finally, the rotational transformation between the conical and body frames is accomplished via
(17)
x^
y^
z^
=
`(a , g)
q^
g^
a^
where
(18)
`(a, g)
=
sin
a cos g
-
sin
g cos a cos g
sin
a sin g cos g cos a sin g
-
cos
a
0
sin
a
3.2 Force Components Due to Radiation Pressure on a Surface
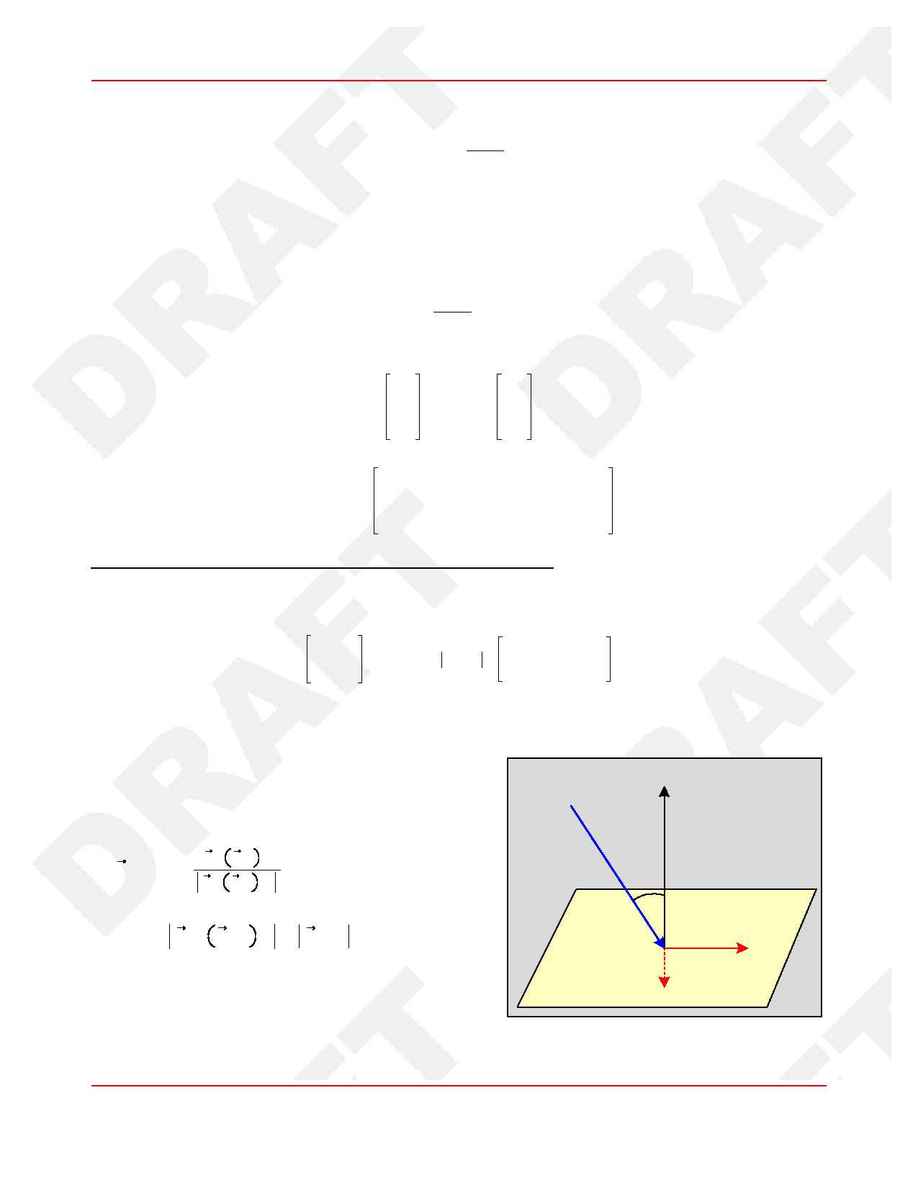
Consider Figure 3, where
is an infinitesimal area on the conical surface. Incident radiation will
d
S
produce perpendicular and parallel force components as shown. We have, by inspection,
(19)
dF
z
dF
y
=
P $ d
S $ cos c $
(1
+
A) cos
c
(1
-
A) sin
c
where A is the surface albedo (i.e., radiation reflection efficiency:
), P is the magnitude of
A c [0, 1]
the incident pressure, and
is the angle between the pressure vector and the surface normal, given by
(20)
cos
c
=
P^ $ N^
Now, in the local conical coordinate frame, the direc-
tion perpendicular to the surface is just
, while the
a^
=
N^
direction parallel to the surface and in the plane defined
by and is
. The denominator of the
P
N^
P
-
P$N^ N^
P
-
P$N^ N^
latter can be written
(21)
P
-
P $ N^ N^
=
P % N^
=
P sin
c
Hence, eq. (19) becomes, in the conical frame,
page 5 of 10
N
P
dF
dF
dS
Figure 3
