When
, this is the statement of conservation of angular momentum about the symmetry axis.
K
z
=
0
Eqs. (11) may be manipulated and expressed as a system of first-order ODEs:
(13)
d
w
dt
=
W
w
d
y
dt
=
W
y
d
h
dt
=
W
h
sin
y d
dt
W
w
=
(1
-
b) W
h
-
(1
+
b) cos y W
w
W
y
+
K
x
sin
h
+
K
y
cos
h
I
xy
d
dt
W
y
=
b cos y W
w
2
-
(1
-
b) W
h
W
w
sin
y
+
K
x
cos
h
-
K
y
sin
h
I
xy
sin
y d
dt
W
h
=
(1
+
b cos
2
y) W
w
-
(1
-
b) cos y W
h
W
y
+
K
z
sin
y
(1
-
b) I
xy
-
K
x
sin
h
+
K
y
cos
h
I
xy
cos
y
The symmetric top equations in the form of eqs. (13) are convenient for implementing in a numerical
program. The program SymTop
3
, discussed later, uses eqs. (13). Applying eqs. (13) to a particular
physical problem consists of specifying the torques, which is the subject of the next section.
3 Torques Due to Pressure Incident on an Attached Truncated Cone
Suppose our symmetric top is in the shape of a cyl-
inder, and that this cylinder is immersed in an envi-
ronment with pressures, for example solar radiation
and solar wind hitting a spacecraft. Further, sup-
pose we shield the spacecraft with a conical skirt
attached at one end of the craft and sweeping back
with cone angle
. The shield is therefore a frus-
tum of a cone, as shown in Figure 2 (sans space-
craft).
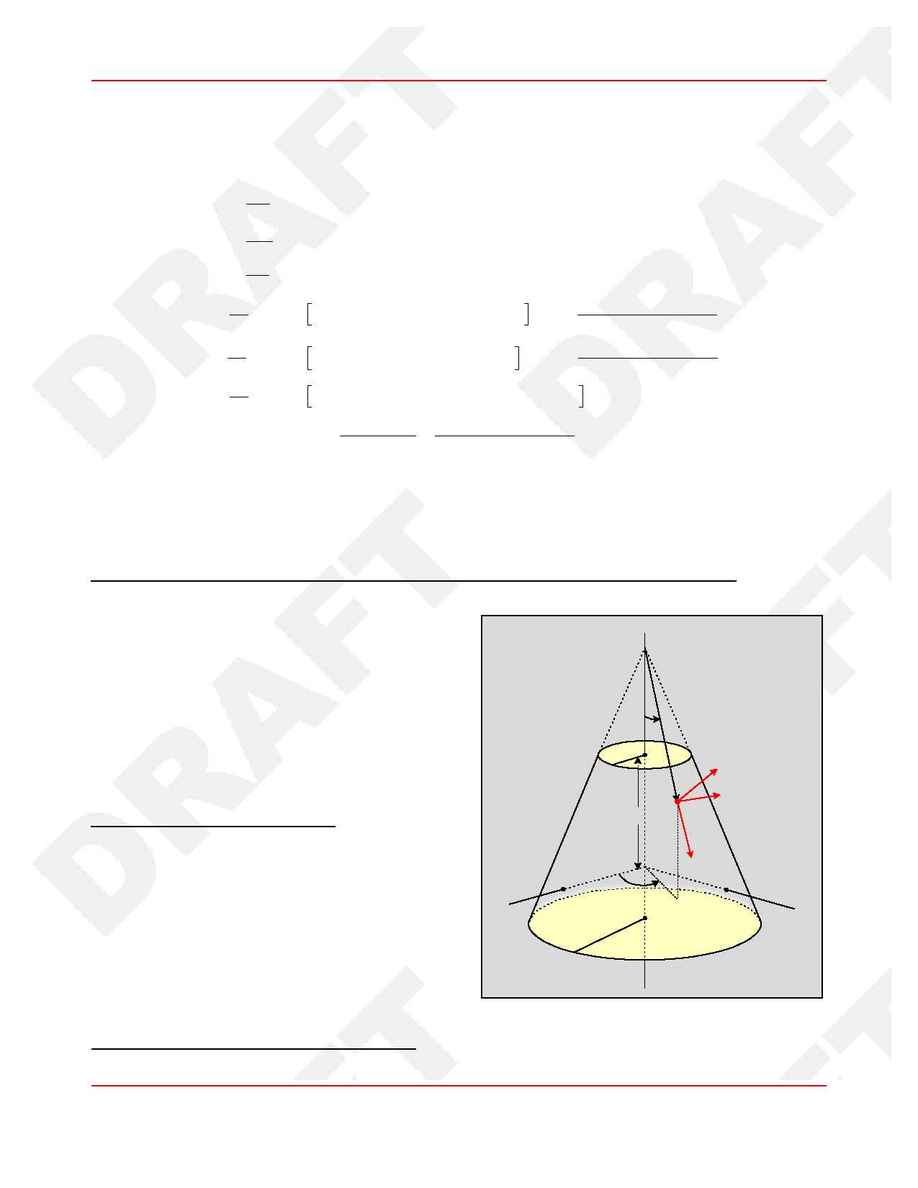
3.1 A Set of Conical Coordinates
For performing integrals of radiation and solar wind
pressure over the conical surface, it will be conven-
ient to define a set of conical coordinates
.
(
q, g, a )
Let the coordinate origin be at the vertex of the
cone, which is a distance d from the top of the frus-
tum, which is in turn a distance h from the center of
mass. Define the set of unit basis vectors
,
(
q^, g^, a^)
as shown in Figure 2.
page 4 of 10
d
h
a
b
z
y
x
f
S
Figure 2
r
3
SymTop is available at
http://aa.usno.navy.mil/SymTop/
