Astronomical Applications Department, U.S. Naval Observatory Precession Memo Page 3
2.3 Rigid Body Equations of Motion
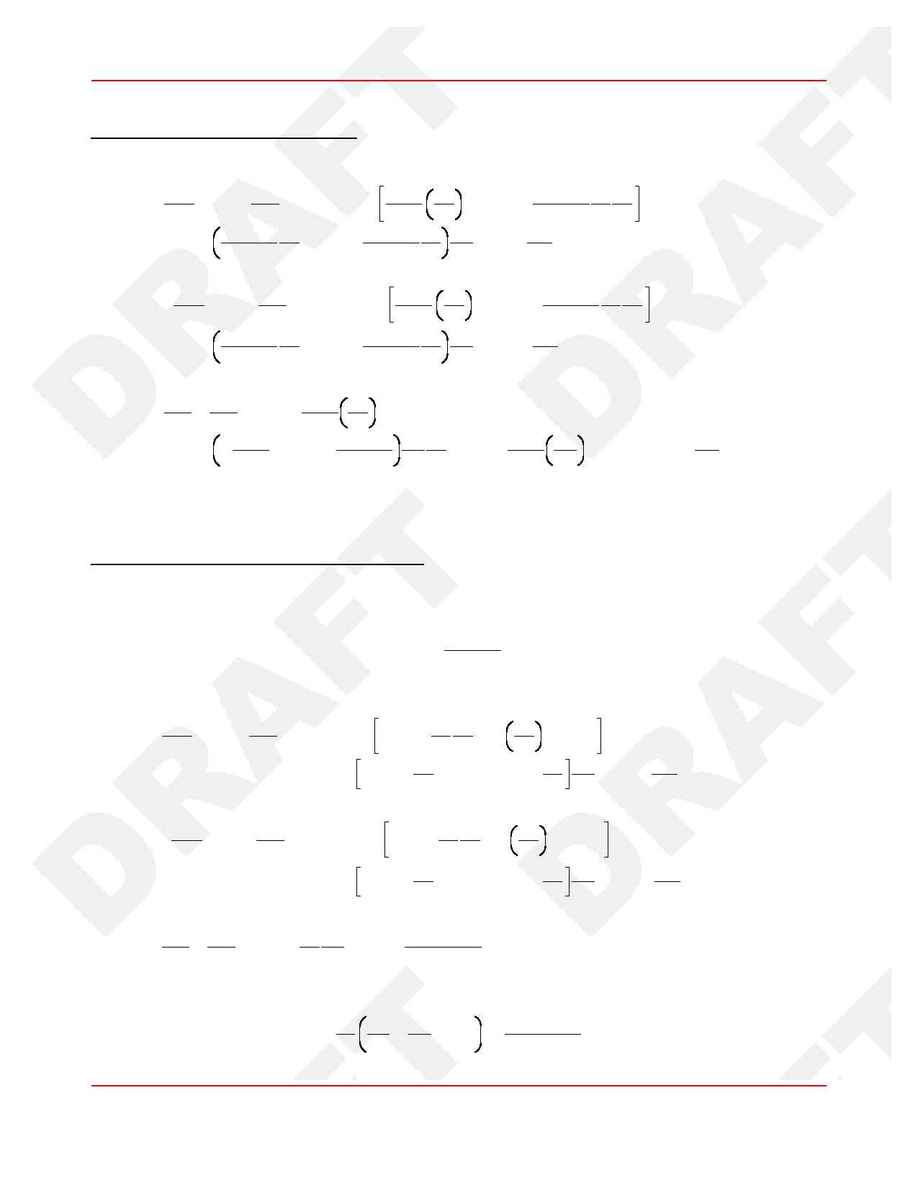
Inserting eq. (8) into the Euler equations (1), we find
(9)
d
2
y
dt
2
cos
h
+
d
2
w
dt
2
sin
h sin y
+
I
z
-
I
y
I
x
d
w
dt
2
cos
y
+
I
x
-
I
y
+
I
z
I
x
d
h
dt
d
w
dt
sin
y cos h
+
I
x
+
I
y
-
I
z
I
x
d
w
dt
cos
y
-
I
x
-
I
y
+
I
z
I
x
d
h
dt
d
y
dt
sin
h
-
K
x
I
x
=
0
-
d
2
y
dt
2
sin
h
+
d
2
w
dt
2
cos
h sin y
+
I
x
-
I
z
I
y
d
w
dt
2
cos
y
+
I
x
-
I
y
-
I
z
I
y
d
h
dt
d
w
dt
sin
y sin h
+
I
x
+
I
y
-
I
z
I
y
d
w
dt
cos
y
+
I
x
-
I
y
-
I
z
I
y
d
h
dt
d
y
dt
cos
h
-
K
y
I
y
=
0
d
2
h
dt
2
+
d
2
w
dt
2
cos
y
-
I
x
-
I
y
I
z
d
w
dt
2
cos
h sin h sin
2
y
+
2
I
x
-
I
y
I
z
sin
2
h
-
I
x
-
I
y
+
I
z
I
z
d
y
dt
d
w
dt
sin
y
+
I
x
-
I
y
I
z
d
y
dt
2
cos
h sin h
-
K
z
I
z
=
0
Eqs. (9) are the rigid body equations of motion expressed in the particular set of Euler angles illus-
trated in Figure 1.
2.4 Equations of Motion for a Symmetric Top
Consider the case where two of the principal moments of inertia are the same, say
.
I
x
=
I
y
h I
xy
Define the ratio
(10)
b h
I
xy
-
I
z
I
xy
Then eqs. (9) become the rigid symmetric top equations of motion,
(11)
d
2
y
dt
2
cos
h
+
d
2
w
dt
2
sin
h sin y
+
(1
-
b)
d
h
dt
d
w
dt
-
b
d
w
dt
2
cos
y sin y cos h
+
(1
+
b)
d
w
dt
cos
y
-
(1
-
b)
d
h
dt
d
y
dt
sin
h
-
K
x
I
xy
=
0
-
d
2
y
dt
2
sin
h
+
d
2
w
dt
2
cos
h sin y
-
(1
-
b)
d
h
dt
d
w
dt
-
b
d
w
dt
2
cos
y sin y sin h
+
(1
+
b)
d
w
dt
cos
y
-
(1
-
b)
d
h
dt
d
y
dt
cos
h
-
K
y
I
xy
=
0
d
2
h
dt
2
+
d
2
w
dt
2
cos
y
-
d
w
dt
d
y
dt
sin
y
-
K
z
(1
-
b) I
xy
=
0
Notice that the third equation of eqs. (11) can be written
(12)
d
dt
d
h
dt
+
d
w
dt
cos
y
=
K
z
(1
-
b) I
xy
page 3 of 10
