We again recover the first-order approximation, this time in eq. (11). So, for all practical pur
-
poses, the first-order approximation is adequate.
Notice that there is no dependence of
on the distance h (cf. Figures 3 and 6). This is because,
as shown by eq. (8), a longitudinal gradient in a homogeneous medium causes an even longitudi
-
nal displacement of a planar surface that is perpendicular to the gradient direction. The term
involving h is of the form
, which is independent of position perpendicular to the z
Ds
=
1
2
h
2
c
axis. Hence it is only the material between z=0 and the mirror surface that contributes to a rota
-
tion of the basic angle. This would seem to indicate that placement of the supports between the
CMA and the optical bench is unimportant, at least for longitudinal temperature gradients. How
-
ever, such is not the case for transverse gradients, as we shall see in Section 3.
2.4. Beam Divergence.
Curvature of the mirrors introduced by the temperature gradient will destroy the collimation of
the input beam upon reflection. In general, the radius of curvature of a function
g(x) is
(16)
R
=
dh
dS
-
1
=
1
+
dg
dx
2
3
2
d
2
g
dx
2
h 2f
where
is the angle of the tangent line at g(x),
is arc length along the curve, and f is the
equivalent focal length. Using
s from eq. (8) in eq. (16) yields
(17)
f
a
=
-
cos
2
x
2c
and
f
b
= -
1
2c
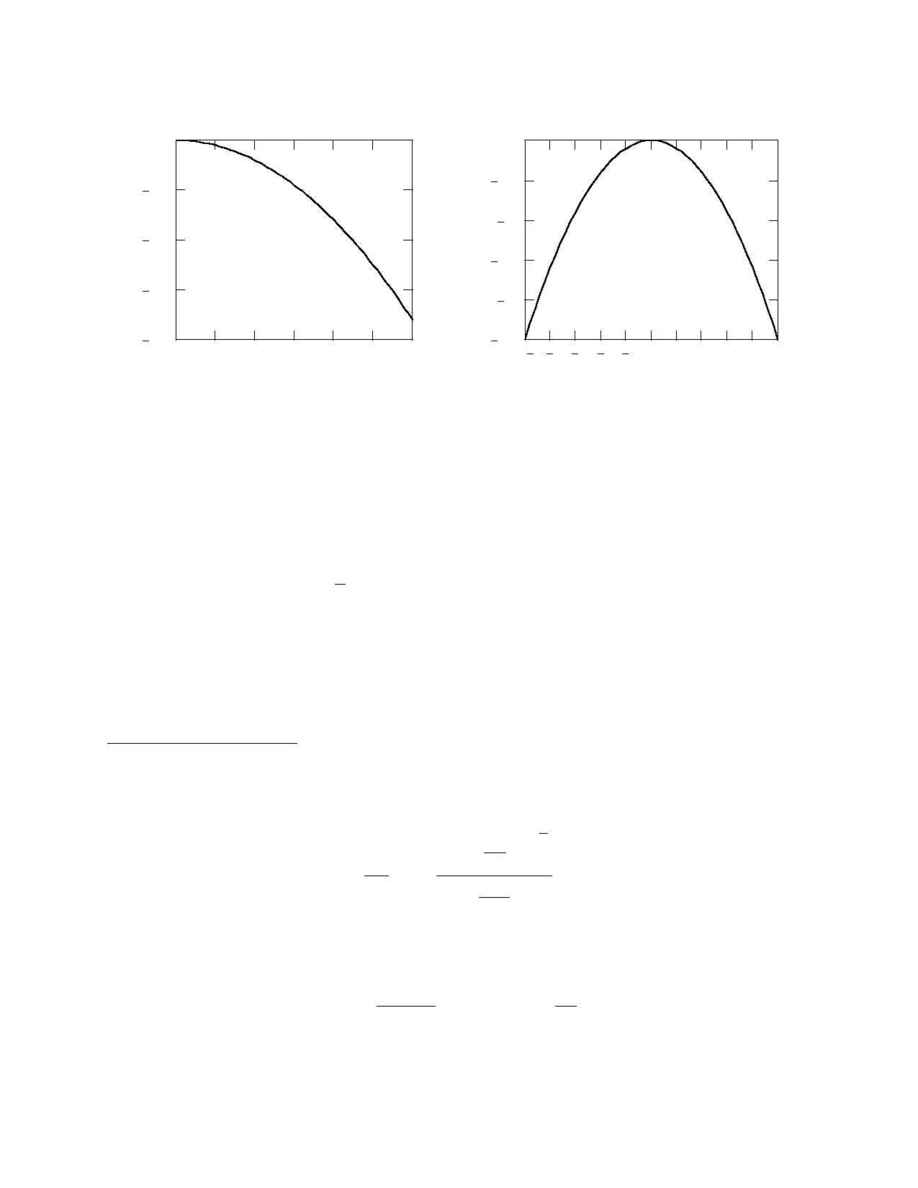
Basic Angle Temperature Gradient Sensitivity
FTM-USNO-95-01
7
0
10
20
30
40
50
60
0.08
0.06
0.04
0.02
0
mirror warp (nm)
x (cm)
5 4
3
2
1
0
1
2
3
4 5
0.25
0.2
0.15
0.1
0.05
0
mirror warp (pm)
y (cm)
s(x=0)
s(y=0)
Figure 5
