Astronomical Applications Department, U.S. Naval Observatory wedges Page 6
cos
2
x
2 a a t
=
5.1 mK
m
A more careful way to determine the change in angle is to average
s across the mirror by inte-
gration. The slope of the tangent along the x direction is
(12)
╣Ds
x, y
╣x
= -
x
cos
2
x c
+
O
c
2
Hence the change in angle averaged over the 2
a by 2b rectangular surface is
(13)
tan
dy
2 l
dy
2
=
1
4 a b
░
0
2a
░
-
b
b
w
x, y
╣Ds
x, y
╣x
dy dx
where w(x,y) is a weighting function. Evaluating the integral with w(x,y)
= 1, we find
(14)
dy
2
= -
a
cos
2
x c
+
O
c
2
To first order we recover the approximate result, eq. (10). The mirror width 2
b only enters in at
second order and is therefore negligible. Solving for
and imposing a basic angle tolerance
,
we have that the temperature gradient constraint is
(15)
b [
cos
2
x
2 a a t
+
O(t
2
)
Basic Angle Temperature Gradient Sensitivity
FTM-USNO-95-01
6
0 2 4
6 8 10
0
10
20
30
40
50
60
0.06
0.04
0.02
0
s
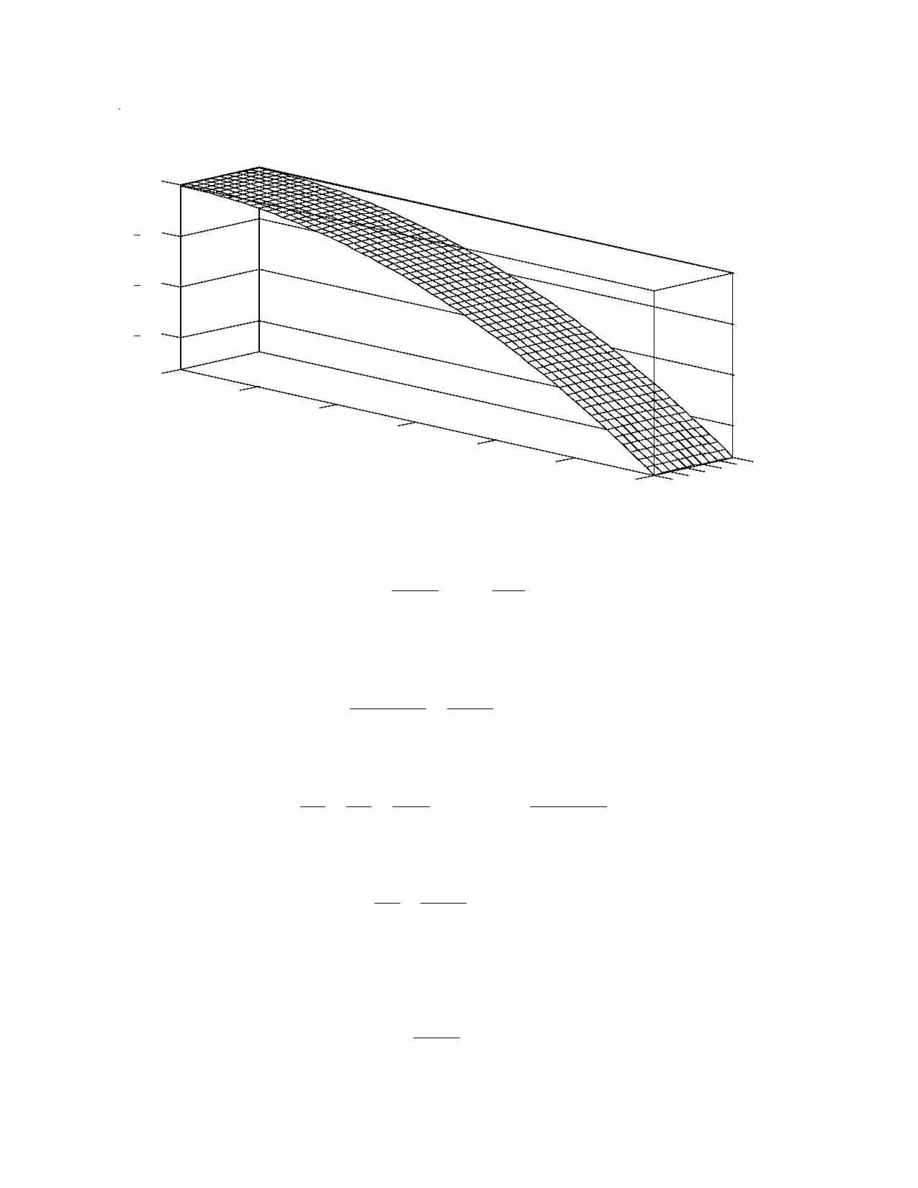
Figure 4
Surface Perturbation
s (nm)
