2. Longitudinal Gradient Case.
2.1. Derivation of the Surface Perturbation.
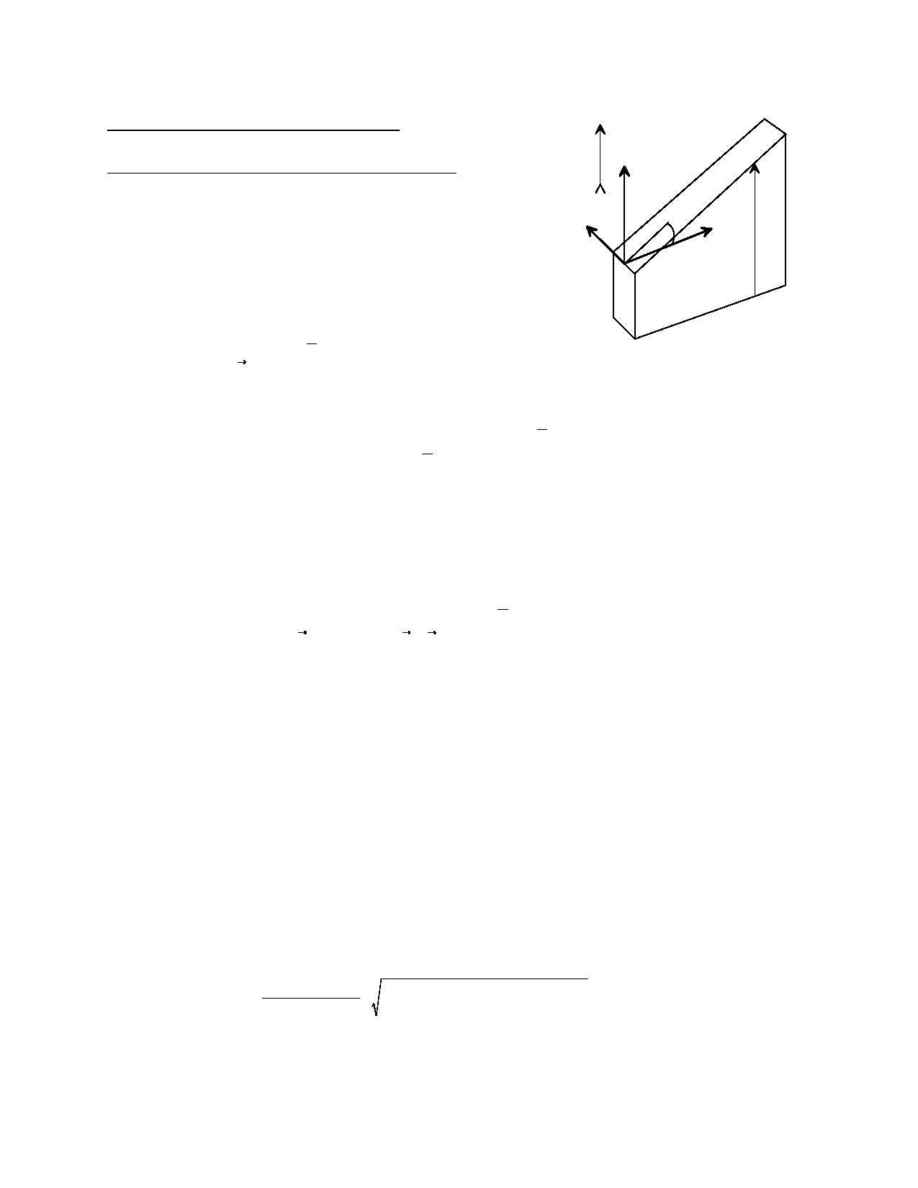
Consider a cylindrical coordinate system
embed-
z, q, h
Æ
ded in a homogeneous medium whose coefficient of ther
-
mal expansion is
°
K
-1
. For a linear temperature gradient
=
dT/dz along the z coordinate axis (Figure 3), the pertur
-
bation of the position of a point in the medium is given by
(1)
u
=
a b
1
2
z
2
-
q
2
z q
0
(R.D. Reasenberg, private communication). In the u
z
term,
arises from linear expansion of
1
2
z
2
the material due to the gradient, while the
component is due to stresses within the material
-
1
2
q
2
set up by the gradient. The latter term is the source of the familiar curling effect of an initially
flat disk. The
term is just the linear expansion of the material, at a height z, in the
u
q
=
a b z q
direction, due to the cumulative effects of a gradient in the z direction. Thus, for a plane inclined
to the direction of the gradient by an angle
, the perturbed position on the initially planar surface
as a function of the unperturbed coordinates is
(2)
r
Â
=
z
Â
q
Â
h
Â
=
r
+
u
=
s
+
1
2
ab
s
2
-
q
2
q
1
+
a b s
h
where
,
, and
is the thickness of the material from the
x
=
q cos h y
=
q sin h
s
=
h
+
q cos h tan x
CMA support(s) along the gradient (Figure 3). In the coordinate system shown in Figure 3, if the
attachment points of the CMA to the optical block are located at z=0, then h=0. More generally,
for attachment at a level z = z
0
, then h = -z
0
.
Equation (2) contains a mix of perturbed and unperturbed coordinates and is therefore not useful
in its current form. We wish to express the perturbed surface in terms of the perturbed coordi
-
nates. From the
' component of (2), we have
(3)
q
Â
=
q
1
+
a b
h
+
q cos h tan x
Solving for
as a function of
', we find
(4)
q
=
1
2c cos h tan x
1
+
c h
2
+
4c q
Â
cos h tan x
-
1
+
c h
where
. The coefficient of thermal expansion is a small quantity, so we can expand on
:
c h a $ b
Basic Angle Temperature Gradient Sensitivity
FTM-USNO-95-01
4
2a
x
y
z
h
2b
s
Figure 3
