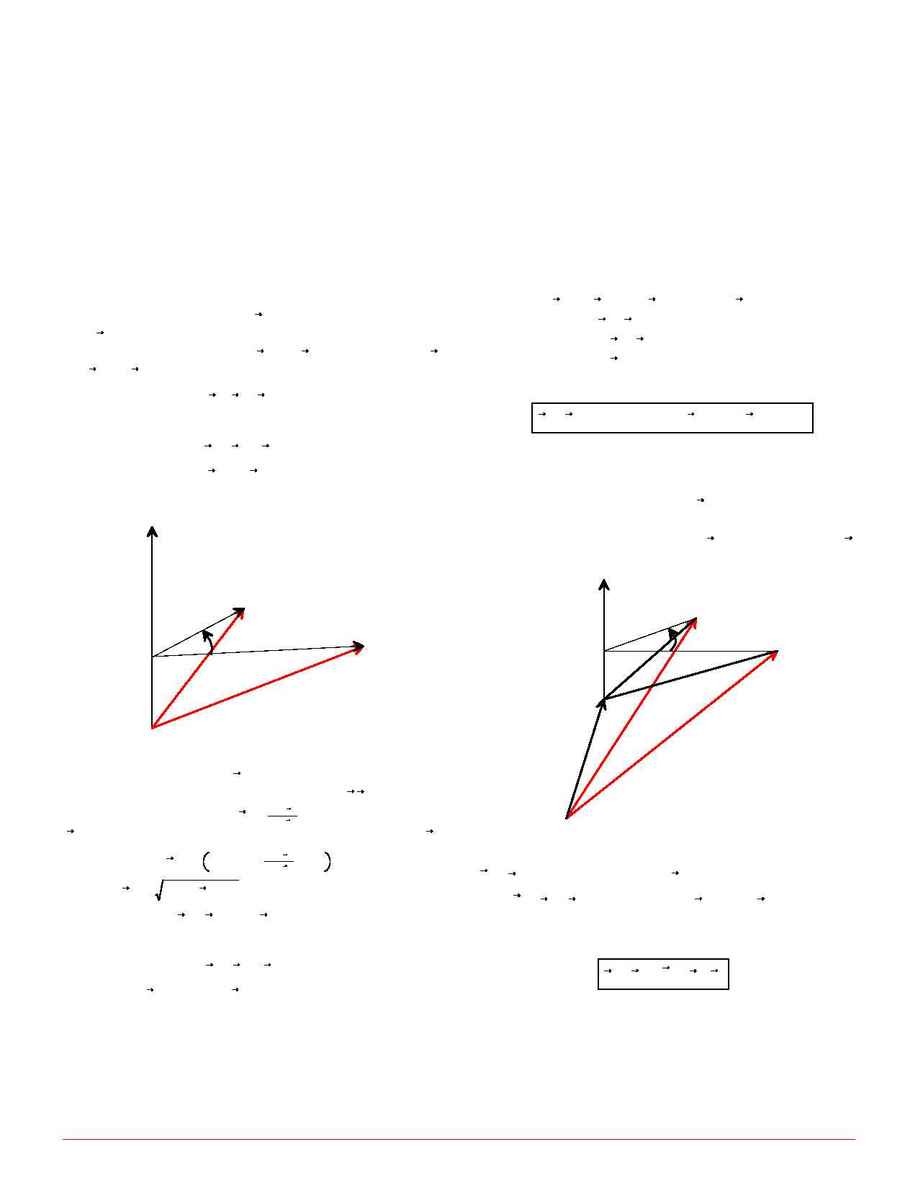
1. ROTATION OF A VECTOR.
We wish to rotate a vector counterclockwise around an
v
axis
by an angle . The geometric picture is illustrated in
w
w
Figure 1. The components of and
perpendicular to
v
v
Â
w
are and
. We have
u
u
Â
(1)
u
=
v
-
(v $ w^) w^
and
(2)
u
Â
=
v
Â
-
(v $ w^) w^
since it is apparent that
.
v $ w^
=
v
Â
$ w^
w
v'
v
u
u'
Figure 1
The trick to determining is to notice that the rotation of
v
Â
the vector is just a coordinate rotation in the
plane. The
u u
Â
unit vector perpendicular to
is
. Hence we can write
u
w^%u
Èw^%uÈ
in terms of its components parallel and perpendicular to ,
u
Â
u
(3)
u
Â
=
u u^ cos
w
+
w^%u
Èw^%uÈ
sin
w
But
, so
Èw^ % uÈ
=
u
2
-
(u $ w^)
2
=
u
(4)
u
Â
=
u cos
w
-
u % w^ sin
w
Now, from (2) we have
(5)
v
Â
=
u
Â
+
(v $ w^) w^
Using (4) for and (1) for , this becomes
u
Â
u
(6)
v
Â
=
u cos
w
-
u % w^ sin
w
+
(v $ w^) w^
=
[v
-
(v $ w^) w^] cos
w
-
[v
-
(v $ w^) w^] % w^ sin
w
+
(v $ w^) w^
Hence we have the result
(7)
v
Â
=
v cos
w
+
(1
-
cos
w)(v $ w^) w^
-
v % w^ sin
w
2. ROTATION OF A POSITION VECTOR AROUND A POINT IN
SPACE.
Now consider a position vector relative to a coordinate
r
origin O. We wish to rotate this position vector counterclock-
wise by and angle around an axis
with anchor point .
w
w
p
See Figure 2.
w
Figure 2
r
r'
p
O
Notice that eq. (7) can be viewed as a linear operator,
, acting on the argument . That is, let
R
w^,
w
(v)
v
(8)
R
w^,
w
(v) h v cos
w
+
(1
-
cos
w)(v $ w^) w^
-
v % w^ sin
w
Then it is apparent from Figure 2 that the rotated position vec-
tor can be written
(9)
r
Â
=
p
+
R
w^,
w
(r
-
p)
HOW TO ROTATE A VECTOR
M
ARC
A. M
URISON
Astronomical Applications Deptartment, U. S. Naval Observatory, Washington, DC
murison@aa.usno.navy.mil
November 23, 1998
ABSTRACT
Rotation of a vector around a direction in space is shown.
Key words: vectors -- vector analysis -- Euclidean geometry
D:\dynamics\text\notes\RotateVector.lwp
MAM 11/23/98 1:16pm
