new set of residuals. This process is iterated until the parameters satisfy
predetermined success criteria.
At the end of the iterative process, we will have produced an ephemeris
that best fits the observations, given the model used, as well as the best-fit
model parameters, formal error estimates of those parameters, and the pa-
rameter cross correlations. The parameter error estimates and parameter
correlations are derived from the partial derivatives and the correlation
matrix from the least squares analysis. Experience with
PEP
has shown
that, normally, at most only a couple or a few iterations are needed
2.5. The Integration Module
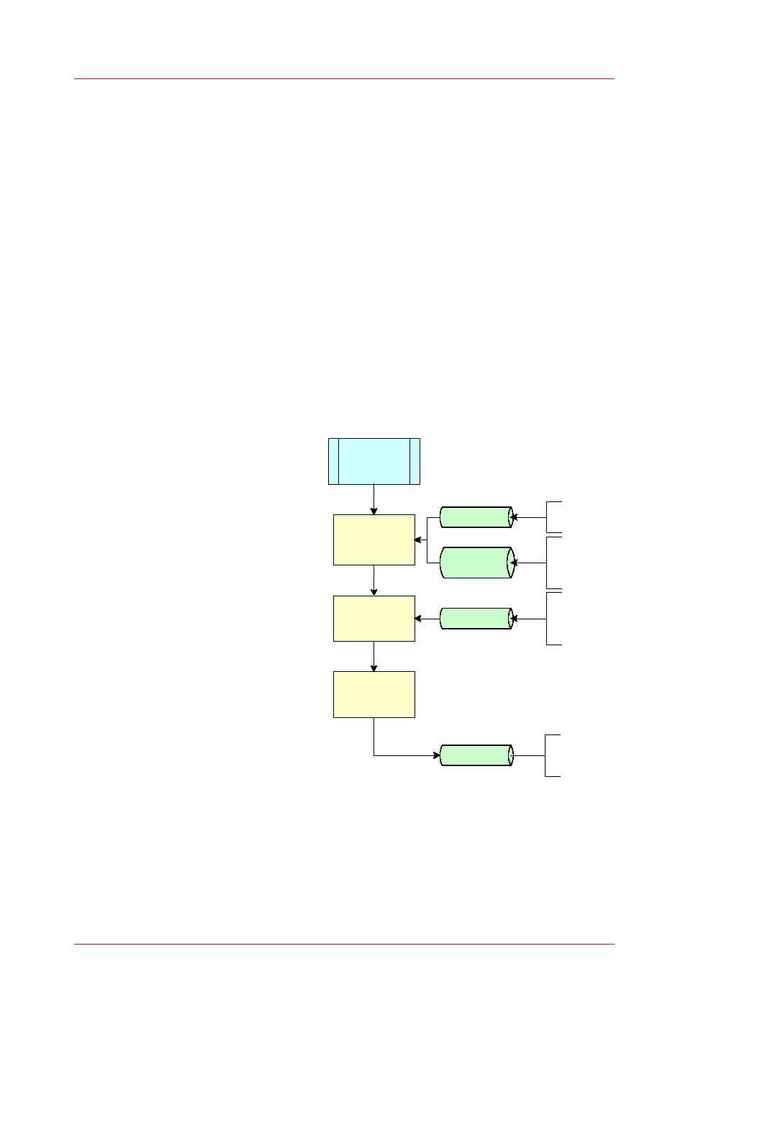
The integration module of Newcomb is relatively straightforward, as
shown in Figure 9. After choosing which bodies to integrate, one sets all
the initial conditions for all the integrated bodies, as well as both the
physical model parameters (G,
masses, etc.) and the integrator
parameters (accuracy limits,
step size limits, etc.). The inte-
grator then integrates the equa-
tions of motion, providing inter-
mediate output along the way.
The intermediate output varies
in complexity, from simple di-
agnostics to runtime graphics of
orbital elements, close ap-
proaches, mean-motion reso-
nance angles, and so on. As
previously mentioned, the inte-
gration module is such an in-
trinsically useful tool that it has
been broken out as a standalone
solar system dynamics applica-
tion, called Newton.
MURISON: MODELING PLANETARY MOTIONS
14 of 20
Figure 9 -- The Integration Module.
Integration
initialize the
physical model
integrate the
equations of
motion
parameters
initial
conditions
ephemeris
- body masses
- gravity model
- planets
- asteroids
- natural satellites
- planetary spins
initialize the
integrator
parameters
- integrator type
- accuracy
- start/stop times
- output interval
- planets
- asteroids
- natural satellites
