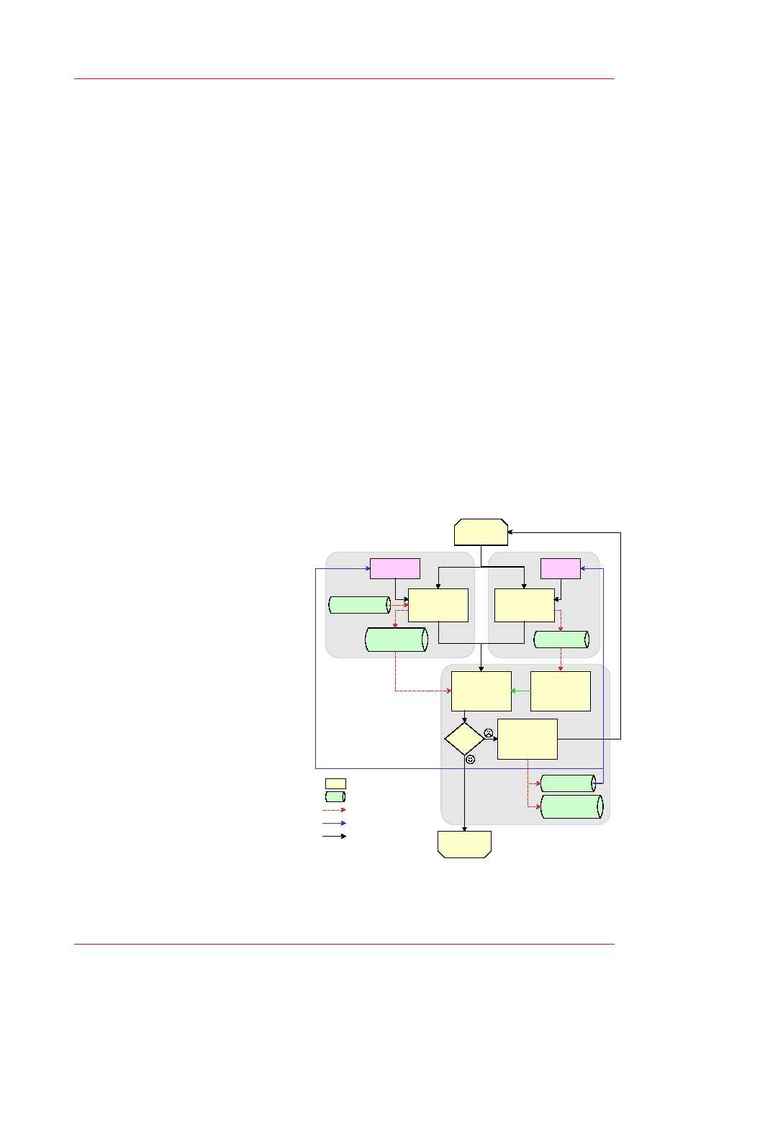
2.4. An Overview of the Newcomb Program Structure
The top level process structure of Newcomb is shown in Figure 8. Basic
operation is as follows.
The observations module is responsible for reading input astrometric ob-
servations and reducing ("massaging") them as necessary. The observa-
tions will be of various types (Figure 5), taken at various observing loca-
tions (Figure 11), including spacecraft. The reduction process corrects for
various instrumental and other effects (e.g. from the atmosphere) that are
specific to a particular set of observations.
The integration module is responsible for numerically integrating a so-
phisticated dynamical model of the solar system -- including general rela-
tivistic terms, a detailed Earth-Moon system, planetary spin vectors includ-
ing precession and nutation, and an unlimited number of asteroids -- to
produce an ephemeris.
The model ephemeris is then compared with the observations in the O-C
section of the parameter adjustment module to produce a set of residuals.
The parameter estimator uses the partial derivatives of the model equations
with respect to the model pa-
rameters (including initial
conditions) to solve the asso-
ciated nonlinear least squares
problem for the most prob-
able set of model parameter
values that minimizes the
O-C residuals.
The adjusted model pa-
rameters are then fed back
into both the ephemeris gen-
erator and the observation
transformation methods. The
data are rereduced as neces-
sary, and a new ephemeris is
generated by the integration
module, using the updated pa-
rameter values. These are
again combined to produce a
MURISON: MODELING PLANETARY MOTIONS
13 of 20
Figure 8 -- Major program processes.
iteration
loop start
massage
observations
integrate eqs.
of motion
form O-C
residuals
parameter
estimator
O-C
eval
iteration
loop end
observations
reduced
observations
ephemeris
parameters
correlation
matrix
observations module
parameter
adjustment
module
integration module
physical
model
observation
models
calculate
observables
data
data flow
process
parameter feedback
process flow
