It has often been observed that orbits near an
invariant surface become "trapped" into almost
regular orbits for long (but finite) times (Perry
and Wiggins, 1994; Kaneko and Konishi, 1994;
also Wisdom, 1983). Jensen (1984, a review)
and Lai et al. (1992, recent work) apply this to
the surviving fraction of un-ionized atoms in a
model of the ionization of surface-state elec-
trons in an oscillating electromagnetic field.
Such "stickiness" will have a profound effect on
the statistical properties of a system, including
diffusion rates or escape rates. A population of
trajectories will contain some members lying
closer than others to a KAM surface, leading to
a distribution of escape times, some of which
will be long.
Perry and Wiggins (1994) show that the
survival probability for an N-degree of freedom
Hamiltonian depends strongly on the dynamics
near the KAM tori. Solutions beginning there
simply take a long time to move away, despite
the fact that the motion is chaotic. They rigor-
ously derive a lower bound on the time it takes
to move away from a torus:
(3)
T m Cr e
(
K b / r
)
a
where T is the lower bound on the time it takes
to double the distance from the surface, r is the
distance from the surface, C and K are positive
constants that depend on the analytic properties
of the Hamiltonian,
> 0 is a measure of the
irrationality of the flow,
= 1/(N+2), and N is
the number of degrees of freedom. The more
irrational the flow (i.e., the higher the reso-
nance order), the more "sticky" is the surface.
Lower bounds like this were first obtained by
Nekhoroshev (1977) for a class of near-
integrable Hamiltonian systems and are there-
fore known as Nekhoroshev type bounds.
They were worked out for the time to move
away from elliptic equilibrium points by Gior-
gilli (1988) and Giorgilli et al. (1989).
The extension to the outer-belt asteroids
follows naturally, and we do not therefore
require the existence of some mysterious, new
class of objects or type of motion in order to
explain the observed behavior. It is, in fact,
quite consistent with the above-mentioned pre-
vious studies. The association with KAM tori
also explains our observation that the outer
asteroid orbits considered here all lie near a
high-order resonance with Jupiter, the main
perturber.
Chaotic Motion in the Outer Asteroid Belt
page 10
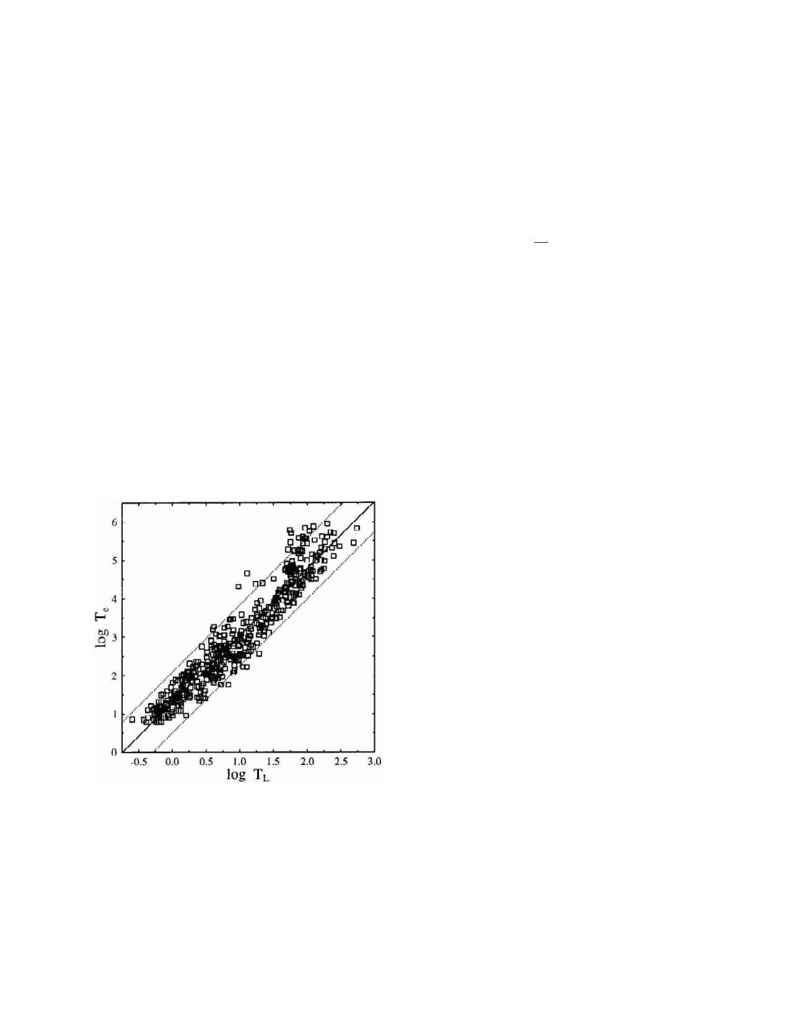
Figure 3.
Log of observed event time, T
e
, vs. the log of
the Lyapunov time, T
L
, for the 440 survey orbits calcu-
lated with m
2
=10 M
J
. The solid line is an unweighted
least squares fit, with slope b=1.74 ▒ 0.03 and intercept
a=1.30 ▒ 0.03. Dotted lines mark the 2
G
boundaries of a
Gaussian fit to the residuals.
