(29)
B h
-
¹x
2
¹a
a
=
a~
and [
M]
ij
h
¹x
2
¹a
i
¹a
j a
=
a~
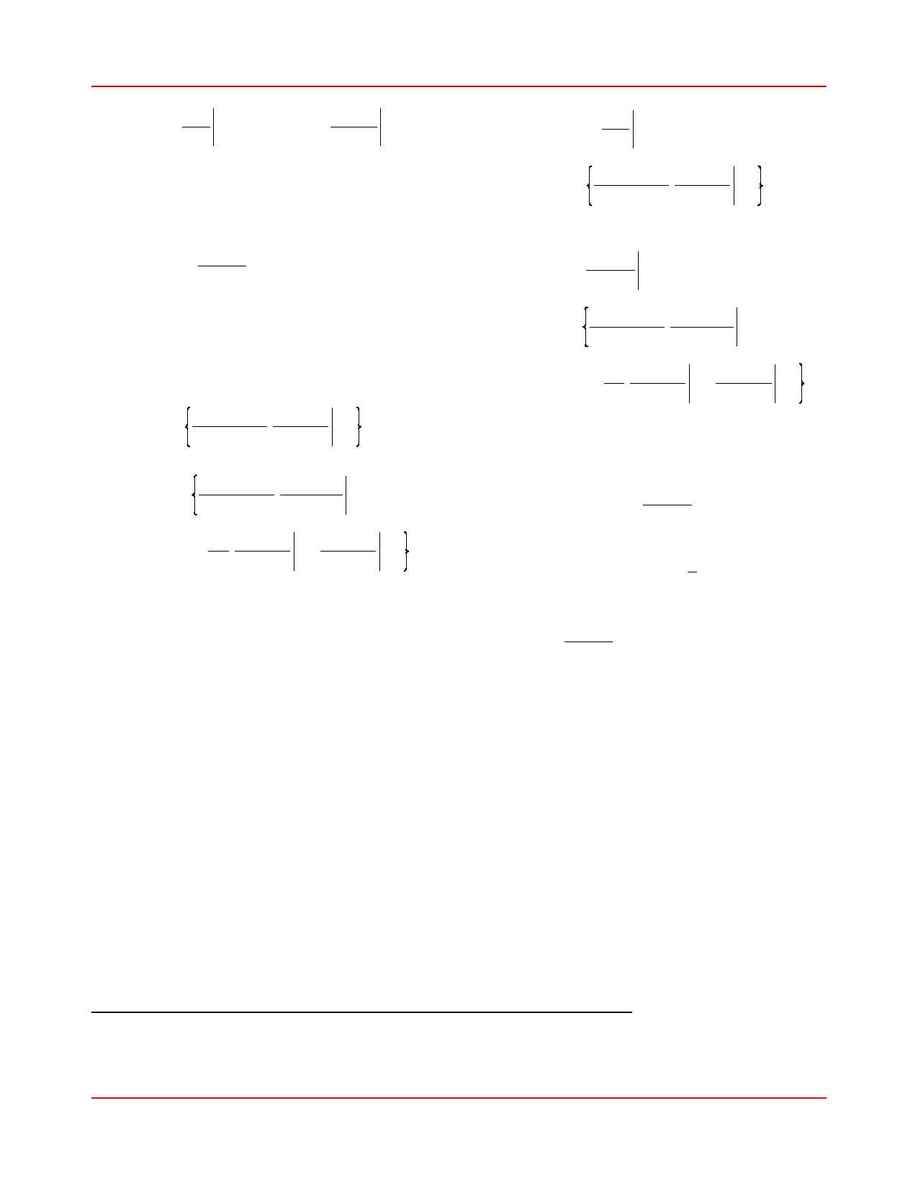
Within the paraboloidal approximation (28), the
correction vector
which minimizes
is given
Da
x
2
(
a)
by the value for which the parameter correction gra-
dient vanishes:
(30)
¹x
2
(
a)
¹Da
l
-
B
+
Da $ M
Hence,
(31)
Da
=
M
-
1
$ B
where we have used the fact that
is symmetric.
M
For
and we calculate
B
M
B
=
y
i
-
y(t
i
,
a)
r
i
2
¹y(t
i
,
a)
¹a
a
=
a~ i
[
M]
jk
=
y
i
-
y(t
i
,
a)
r
i
2
¹
2
y(t
i
,
a)
¹a
j
¹a
k
a
=
a~
-
1
r
i
2
¹y(t
i
,
a)
¹a
j
a
=
a~
¹y(t
i
,
a)
¹a
k
a
=
a~ i
(32)
Unfortunately, although the merit function is
unitless, the elements of eqs. (32) are not (in
general). This can lead too easily to an ill-
conditioned matrix
when the parameters exhibit
M
numerically widely disparate units. Following
Hessler
et al.
3
, let us redefine
and in a unitless
B
M
fashion:
(33)
B
k
h
-
a~
k
¹x
2
¹a
k a
=
a~
=
a~
k
y
i
-
y(t
i
,
a)
r
i
2
¹y(t
i
,
a)
¹a
k
a
=
a~ i
and
[
M]
jk
h a~
j
a~
k
¹x
2
¹a
j
¹a
k a
=
a~
=
a~
j
a~
k
y
i
-
y(t
i
,
a)
r
i
2
¹
2
y(t
i
,
a)
¹a
j
¹a
k
a
=
a~
-
1
r
i
2
¹y(t
i
,
a)
¹a
j
a
=
a~
¹y(t
i
,
a)
¹a
k
a
=
a~ i
(34)
To keep a unitless form for the merit function,
define
(35)
da
k
h a
k
-
a~
k
a~
k
Using (33) and (34), we can rewrite (28) as
(36)
x
2
(
a) l x
2
(
a~)
-
da $ B
+
1
2
da $ M $ da
Requiring
(37)
¹x
2
(
a)
¹ da
l
-
B
+
da $ M
=
0
we have, finally,
(38)
da
=
M
-
1
$ B
where and
are given by (33) and (34). Notice
B
M
that the form of eqs. (38) is identical to that of eqs.
(13). The procedure, then, is to start with an initial
set of values for the parameters, calculate the correc-
tion via eqs. (38), correct the parameter values, and
repeat until the values stop changing significantly.
Chapter 3: Parameter Adjustment
D:\Newcomb\Documentation\NewcombManual.lwp
12 of 19
10:42pm April 23, 1997
3
J.P. Hessler, D.H. Current, and P.J. Ogren (1996), "A new scheme for calculating weights and describing correlations in
nonlinear least-squares fits",
Computers in Physics 10, 186.
